Área na malha quadriculada

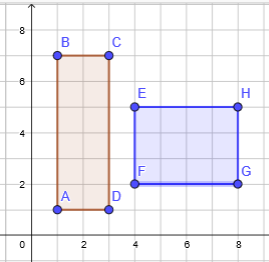
1. Desenhe dois retângulos:

· vértices A (1;1), B (1;7), C (3;7) e D (3;1)

· vértices E (4;5), F (4;2), G (8;2) e H (8;5)

a. Complete a tabela:

b. Escreva uma fórmula que relacione a área (A), a base (b) e a altura (h) de um retângulo.

2. Desenhe dois paralelogramos:

· vértices A (1;1), B (4;7), C (6;7) e D (3;1)

· vértices E (7;5), F (10;2), G (14;2) e H (11;5)

a. Complete a tabela:

b. Escreva uma fórmula que relacione a área (A), a base (b) e a altura (h) de um retângulo paralelogramo.

3. Desenhe o losango de vértices A (2;5), B (5;9), C (5;8) e D (5;1)

a. Trace a diagonal maior BD e a diagonal menor AC

b. Pinte cada um dos quatro triângulos de cores diferentes.

c. Desenhe outro losango idêntico ao anterior e recorte cada triângulo colorido para formar peças de quebra-cabeça.

d. Construa um retângulo com as 4 peças. Cole este retângulo ao lado do primeiro losango.

e. Complete a tabela:

f. Escreva uma fórmula que relacione a Área (A), a diagonal maior (D) e a diagonal menor (d) de um losango.

4. Desenhe o trapézio de vértices A (2; 1), B (2; 4), C (4; 4) e D (6; 1)

a. Desenhe outro trapézio idêntico ao anterior e recorte.

b. Cole o segundo trapézio sobre o primeiro de modo a construir um retângulo.

c. Complete a tabela:

d. Escreva uma fórmula que relacione a Área (A), a base maior (B) e a base menor (b) de um trapézio.

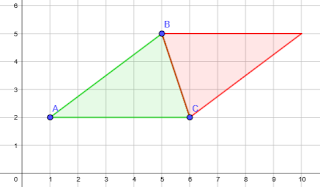
5. Desenhe o triângulo de vértices A (1; 2), B (5; 5) e C (6; 2).

a. Desenhe outro triângulo idêntico ao anterior e recorte.

b. Cole o segundo triângulo sobre o primeiro de modo a construir um paralelogramo.

c. Complete a tabela:

d. Escreva uma fórmula que relacione a Área (A), a base (B) e a altura (h) de um triângulo.

Lição de casa

· Compreender e usar o plano cartesiano para representação de pares ordenados.

· Calcular área de polígonos de diferentes tipos.