Arquivo para impressão (
clique aqui)
8°
ano - Lista de Exercícios – Área de figuras planas
1.
Calcule a área dos polígonos:
2.
Determine a área
das figuras abaixo:
a.
Triângulo cuja base mede 8cm e altura mede 5,2
cm
b.
Paralelogramo cuja a base mede 10 cm e a altura
é a metade da medida da base
c.
Triângulo de base 18 cm e altura igual a 2/3 da
medida da base.
d.
Trapézio de base menor igual a 2cm, base maior
igual a 3cm e a altura igual a 10cm
e.
Trapézio cuja a base maior mede 24 cm, base
menor é igual a 16 cm e a medida da altura é igual à metade da medida da base menor.
3.
Calcule a área dos polígonos:
4.
Um piso quadrado de cerâmica tem 15 cm de lado. Quantos
pisos são necessários para assoalhar uma sala de 45m² de área?
5.
Um vitral é composto de 80 peças triangulares
iguais, de base 25cm e altura 16 cm. Qual é a área desse vitral?
6.
O pátio de uma escola tem a forma retangular e
suas dimensões são 40m e 32m. Nesse pátio foi construída uma quadra de
basquete. Sabendo-se que as medidas oficiais de uma quadra de basquete são 20m
por 12, qual a área livre que restou desse pátio?
7.
Uma parede tem 8 m de comprimento por 2,75m de
altura. Com uma lata de tinta é possível pintar 10m² de parede. Quantas latas
de tinta serão necessárias para pintar essa parede?
8.
Um campo de futebol tem 105m de comprimento e 70m
de largura. Para gramar esse campo foram compradas placas de grama. Cada placa
pode cobrir uma área de 3,50 m². Quantas placas de grama foram compradas para
gramar o campo todo?
9.
Sabendo que a área de um quadrado é 36cm², qual
é o seu perímetro?
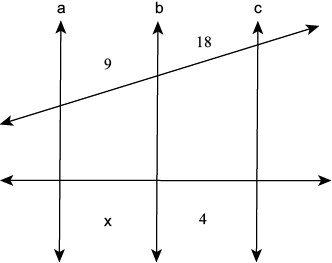
10.
Calcule a área das figuras:
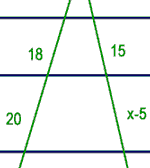
11.
A área do trapézio abaixo é 48 m². Calcule o
valor de x.
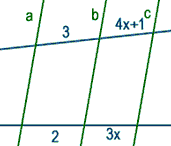
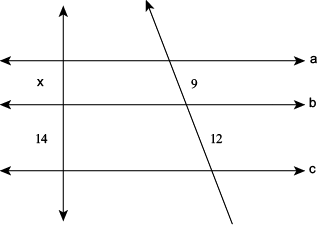
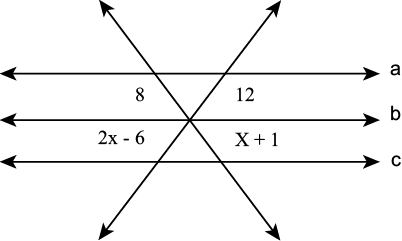
12.
Conhecendo o valor da área de cada
paralelogramo, descubra o valor de x:
13.
O retângulo e o quadrado da figura têm o mesmo perímetro.
a.
Qual o lado do quadrado?
b.
Qual a área do quadrado?
|
|
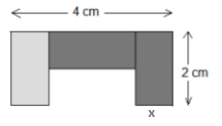
14.
A figura é constituída por três retângulos
geometricamente iguais.
a.
Qual é a medida de x?
b.
Qual a área da zona escura?
c.
Qual o perímetro de toda a figura?
|
|
15.
No chão da sala de Matilde há um tapete com a
forma de um quadrado. O perímetro do tapete é 20m. A área do chão da sala é
31m². Calcule a área da parte do chão da sala que não está coberta pelo tapete.
16.
Calcule a medida de base de um triângulo de área
48 m² sabendo que a altura mede 8m.
17.
O perímetro de um retângulo é 48 cm. A medida do
lado maior é o triplo da medida do lado menor. Qual a área deste retângulo?
18.
Um salão quadrado com 4,5m de lado será
revestido com piso. O dono do salão já possui 12,75m² de piso, e sabe que não
será suficiente para revestir todo o salão. Quantos m² de piso ele precisa
ainda comprar?
19.
A área do trapézio da figura ao lado mede 42 cm²
e sua altura 3 cm. Calcule o valor de x.
20.
Calcule a área da figura sombreada, sabendo que
o lado do quadrado maior mede 8m e do quadrado menor 5 m

21.
A figura a seguir é composta de triângulos
equiláteros de lado l = 3 cm. Se adotarmos que estes triângulos têm altura
aproximada de 2,6 cm, qual a área total da figura?

22.
A área do quadrado seguinte é 49 cm². Qual o valor
de x?

23.
Um quadrado cuja medida do lado é (x + k) tem
área dada por x² + 8x + 16. Qual o
valor de k?

24.
Ulisses gosta de cultivar flores. Como no
quintal de sua casa há um espaço disponível, junto ao muro do fundo, ele deseja
construir um pequeno canteiro retangular e, para cercar os três lados
restantes, pretende utilizar os 40 m de tela de arame que possui. Como ainda
está indeciso quanto as medidas, fez o seguinte desenho. Quais as medidas dos
lados do canteiro para que sua área seja de 200m² ?

Gabarito
1-)
a-) 4,5 cm²
b-) 12 cm²
c-) 15,75 cm²
d-) 3,75 cm²
e-) 10,825 cm²
2-)
a-) 20,8 cm²
b-) 50 cm²
c-) 108 cm²
d-) 25 cm²
e-) 160 cm²
3-)
a-) 24 cm²
b-) 40 cm²
c-) 40 cm²
d-) 18 cm²
4-) 2000 pisos
5-) 16000 cm²
6-) 1040 m²
7-) 3 latas (2,2 latas)
8-) 2100 placas
9-) 24 cm
10-)
a-) 64 cm²
b-) 60 cm²
c-) 64 cm²
d-) 24 cm²
e-) 26,5 cm²
11-) 6
12-)
a-) 16 cm
b-) 24 cm
13-)
a-) 11 cm
b-) 121 cm
14-)
a-) 1 cm
b-) 2 cm²
c-) 14 cm
15-) 6 m²
16-) 12 m²
17-) 36 cm²
18-) 7,5 m²
19-) 13 cm
20-) 39 m²
21-) 15,6 cm²
22-) 5 cm²
23-) k = 4
24-) x = 10 m, y = 20 m






.jpg)







.jpg)